Notation Key
- Vectors: boldface
- Scalars: normal font
- X₂: second data record
- X₂: second component of dataset
- Number of data records: n
- "Star" for true quantity, e.g., θ*
- "Hat" for estimates, e.g., θ̂
- Upper case: random variables, e.g., Y
- Lower case: numbers and constants, e.g., y for realized value of Y
New Insights
To find relationships between different variables to get new patterns.
Regression Framework
Vector X₁ | Y₁Dimension m : | :Data : | :Xₙ | Yₙ---+---X | Y? ← Scalar
Regressor/predictor: Ŷ = g(X)
Goal: Build function g so when a new X comes in, we can output predicted value Ŷ. X → [g] → Ŷ
We need to learn a good g from the data.
Objective Function
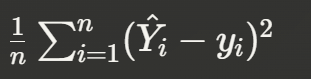
Where:
- g(Xᵢ) is the prediction
- Yᵢ is the actual value
- g(Xᵢ) - Yᵢ is the error, which we want to be small
- The whole function is mean square error (MSE)
Overfitting Warning
If it's an arbitrary curve (a line that goes through all data points, so the error is 0), we can't believe it. This is called overfitting, which we need to avoid since it leads to nonsensical conclusions.
[Graph showing overfitting: A wiggly line that perfectly passes through all points, versus a simpler linear fit]
Linear Regression Model
We prohibit g to be arbitrary general, restrict to limited class of predictors:
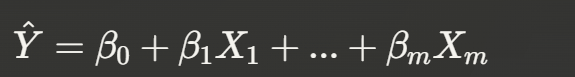
Within linear regression, we restrict to the class of predictors that are linear in the attributes in the X vector.
When a person comes in with X₁ up to Xₘ, then form a linear combination of these attributes.
Choice of predictor β = curve in 2D β determines the location of that line.
The slope here would be β₁. By playing with β, we can move the line around.
Residuals
Residual is an error between predicted value and the observed value.
We need to find θ so the sum of squared residuals is as small as possible:
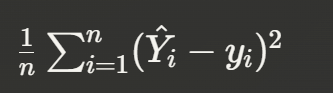
Any line gives certain numerical value for the sum of squared residuals. This is called ordinary least squares (OLS).
Assumptions of Linear Regression
- Linearity - The regression model can be expressed linearly
- Homoscedasticity - The variance of the error is constant
- Independence - Observations are independent from each other
- No autocorrelation
Example Application
- n = 209
- m+1 = 4
- β₀ is the intercept
- θ̂ = [2.94, 0.064, 0.19, -0.001]ᵀ
- Sales = 2.94 + 0.064(TV) + 0.19(Radio) - 0.001(Newspaper)
Linear regression software produces the coefficients that multiply the ads expenditure over different channels.
-0.001 is unusual as it suggests the more you spend, the lower the sales.
Simple linear regression example: Sales = 12.35 + 0.055(Newspaper)
0.055 contradicts with -0.001, so which one is true?



Comments NOTHING